考德上“行测天天练”——第二课时，年龄问题（解析）

第二课时，年龄问题(解析)

1解析：【B】设今年哥哥X岁、弟弟Y岁 ，年龄差是X-Y则有方程组X+Y=35 哥哥在弟弟这么大时哥哥的年龄能表示为：X-(X-Y)、弟弟的年龄可表示为：Y-(X-Y) 。X+Y=35 X=21X-(X-Y)]=2[Y-(X-Y)] Y=14

2,解析：【C】73-4×4=57,但题中又说是58，那么，儿子的没有加上去，说明4年前儿子还没有出生，所以现在儿子的岁数为：73-3×4-58=3岁，那么现在女儿5岁。

3,解析：【C】可以假设姐姐年龄为X，姐姐与妹妹的年龄差是d，那么x+x+d=48+d+2，得到x=25，也就是说姐姐今年25岁。

4,解析：【C】设甲、乙、丙分别为：X、Y、Z人。38X+24Y=30(X+Y);24Y+42Z=34×(Y+Z)由上面可算得X:Y=3:4，Y:Z=4:5，故X,Y,Z=3:4:5，最后利用平均数公式求得平均年龄为(38×3+24×4+42×5)÷12=35。

5,解析：【C】长孙，次孙，幼孙现在的年龄和是20+13+7=40，如果设X年后三个孙子的年龄之和与祖父的年龄相等，则祖父的年龄增加了X岁，而三个孙子的年龄和增加了3X岁，故：70+X=40+3X可解X=15。

6解析：【D】(解析一)：设甲今年为X、乙为Y岁。X=4Y;X+4=3×(Y+4);X=32,Y=8，所以2000年甲、分别为34、10。解析二：代入排除法。将选项代入条件甲的年龄减去2是乙的年龄减去2的4倍，可知D项符合条件。

7,解析：【C】把四个数加起来，正好相当于把每个人算了3次，因此四个人的年龄和为(55+58+62+65)÷3=80，那么年龄最小的为80-65=15岁。

8,解析：【C】设哥哥今年的年龄为X，弟弟今年的年龄为Y，则5年后哥哥的年龄是X+5,(X+5)+(Y-3)=29 X=15Y=4×(X—Y) Y=12三年前弟弟的年龄是X-3。由题意得。故哥哥的年龄是15，弟弟的年龄是12.

9,解析：【B】(解析一)设甲、乙现在为X、Y，利用年龄差相等：X-Y=Y-4;67-X=X-Y，X=46;Y=25。(解析二)等差数列法：根据年龄差不变可知，67、X、Y、4就够成了等差数列，67与4之间被平均分成了三段：显然，4与67相隔63，长度被平均分成了3段，每段长各21，即可算得X=46,Y=25。

8,解析：【C】设哥哥今年的年龄为X，弟弟今年的年龄为Y，则5年后哥哥的年龄是X+5,(X+5)+(Y-3)=29 X=15Y=4×(X—Y) Y=12三年前弟弟的年龄是X-3。由题意得。故哥哥的年龄是15，弟弟的年龄是12.

9,解析：【B】(解析一)设甲、乙现在为X、Y，利用年龄差相等：X-Y=Y-4;67-X=X-Y，X=46;Y=25。(解析二)等差数列法：根据年龄差不变可知，67、X、Y、4就够成了等差数列，即67与4之间被平均分成了三段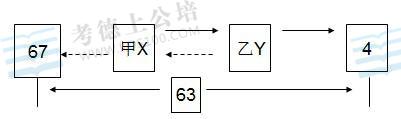：显然，4与67相隔63，长度被平均分成了3段，每段长各21，即可算得X=46,Y=25。